Introduction à la cryptographie
ArticleCategory:
System Administration
AuthorImage:

TranslationInfo:[Author and translation history]
original in fr Pierre Loidreau
AboutTheAuthor
Pierre est Enseignant-Chercheur à l'ENSTA (Ecole Nationale
Supérieure de Techniques Avancées). Son domaine de recherche concerne
les "cryptosystèmes" fondés sur la théorie des codes correcteurs d'erreurs. Il
pratique Linux tous les jours... et le tennis fréquemment.
Abstract:
Cet article a été publié dans un numéro spécial sur la sécurité de Linux
Magazine France. L'éditeur, les auteurs, les traducteurs ont aimablement
accepté que tous les articles de ce numéro hors-série soient publiés dans
LinuxFocus. En conséquence, LinuxFocus vous "offrira" ces articles au fur et
à mesure de leur traduction en Anglais. Merci à toutes les personnes qui se
sont investies dans ce travail. Ce résumé sera reproduit pour chaque article
ayant la même origine.
ArticleIllustration:

ArticleBody:[The article body]
Pourquoi la cryptographie - 2500 ans d'histoire avérée.
L'origine de la cryptographie remonte sans doute aux origines de
l'homme, dès que ceux-ci apprirent à communiquer. Alors, ils durent
trouver des moyens d'assurer la confidentialité d'une partie de leurs
communications. Dans l'Égypte ancienne, l'écriture joua parfois ce
rôle. Cependant la première attestation de l'utilisation délibérée de
moyens techniques permettant de chiffrer les messages vint de la
Grèce, vers le VIème siècle avant J.C, et se nomme ``scytale''. Le
scytale était un bâton. L'expéditeur enroulait une bandelette autour
et écrivait longitudinalement sur le bâton. Puis il déroulait la
bandelette et l'expédiait au destinataire. Sans la connaissance du
diamètre du bâton qui jouait le rôle de clé, il était impossible de
déchiffrer le message.
Plus tard, les armées romaines utilisèrent pour communiquer le
chiffrement de César consistant en un décalage de l'alphabet de trois
lettres.
Puis, pendant près de 19 siècles, on assista au développement plus ou
moins ingénieux de techniques de chiffrement expérimentales dont la
sécurité reposait essentiellement dans la confiance que leur
accordaient les utilisateurs. Au 19ème siècle, Kerchoffs posa les
principes de la cryptographie moderne. L'un des principaux pose que
la sécurité d'un système de chiffrement ne résidait que dans la clé et
non dans le procédé de chiffrement.
Désormais, concevoir des systèmes cryptographiques devait
répondre à ces critères. Cependant,
il manquait encore à ces systèmes une assise mathématique donnant des
outils qui permette de mesurer,
de quantifier leur résistance à d'éventuelles attaques, et pourquoi pas de trouver le ``saint Graal'' de la cryptographie : le système inconditionnellement sûr. En 1948 et 1949, deux articles de Claude Shannon,
``A mathematical theory of communication'' et surtout
``The communication theory of secrecy systems'' donnèrent des assises scientifiques à la cryptographie en balayant espoirs et préjugés. Shannon prouva que le chiffrement de Vernam introduit quelques dizaines d'années plus tôt -- encore appelé one-time pad -- était le seul système inconditionnellement sûr. Cependant ce système est impraticable. C'est pourquoi, de nos jours pour évaluer la sécurité d'un système on s'intéresse plutôt à la sécurité calculatoire. On dit qu'un système de chiffrement à clé secrète est sûr si aucune attaque connue ne fait beaucoup mieux en complexité que la recherche exhaustive sur l'espace des clés.
L'AES (Advanced Encryption Standard)
Très récemment, en octobre 2000, un nouveau standard de chiffrement à clé secrète fut élu parmi
15 candidats par la NIST (National Institute of Standards and Technology) afin de remplacer le viellissant DES dont la taille des clés devenait trop petite. L'algorithme choisit pour devenir l'AES est le Rijndael, du nom
condensé de ses concepteurs, Rijmen et Daemen.
Celui-ci est un système de chiffrement dit ``par blocs'' car les
messages sont chiffrés par blocs entiers, qui ici sont de 128 bits.
Il existe plusieurs versions du système utilisant des clés de 128, 192
ou 256 bits.
Pour information, le DES chiffre des blocs de 64 bits avec une clé de
56 bits seulement. Le triple DES utilisé communément jusqu'alors chiffre des blocs de
64 bits avec une clé de 112 bits.
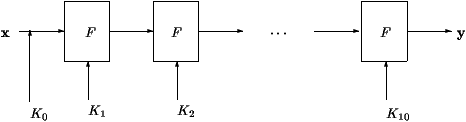
Table 1: Itérations de l'AES
Le principe de fonctionnement de l'AES est décrit dans la figure 1.
En premier lieu, on ajoute bit à bit le message avec la clé secrète K0.
Puis, comme pour tous les algorithmes de chiffrement
par blocs, on itère une fonction F, paramétrée par des sous-clés qui sont obtenues de la clé
maître par un algorithme de cadencement de clés.
Dans le cas d'AES, on itère 10 fois la fonction F.
- La fonction F itérée lors du chiffrement est décrite figure 2. Celle-ci
prend en entrée des blocs de 128 bits répartis sur 16 octets. Tout d'abord, on applique à
chaque octet la même permutation S. Ensuite on applique aux 16 octets
une seconde permutation P. Au résultat obtenu, on ajoute alors bit
à bit la sous-clé de 128 bits obtenue par l'algorithme de cadencement de clé.
- L'algorithme de cadencement de clé permet de calculer la clé Ki du iéme tour en fonction
de la sous-clé Ki-1 du (i-1)ème tour, K0 étant la
clé secrète. Celui-ci est décrit dans la figure 3.
Les 16 octets de la clé Ki-1 sont pris 4 à 4. Aux 4 derniers octets, on commence par
faire subir une permutation, puis on réutilise la même permutation S que celle de la
fonction F afin de permuter les bits de chaque octet. Ensuite, on additionne au premier octet du
nouvel ensemble l'élément ai. Cet élément
est un octet qui dépend du numéro i du tour considéré.
Enfin pour obtenir Ki, on ajoute bit à bit les 4 octets
obtenus aux 4 premiers octets de Ki-1, puis le résultat obtenu est additionné aux 4 octets suivants et ainsi de suite.
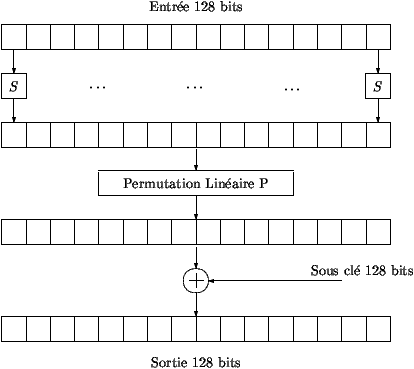
Table 2: Fonction F
Voici brièvement comment sont construites les permutations et à quoi correspond
la constante ai. Techniquement et
pour des soucis de facilités, un octet peut être considéré comme un élément d'un
ensemble à 256 éléments appelé corps fini,
sur lequel existent toutes sortes d'opérations simples, notamment des opérations d'additions, de multiplication et d'inversion. La permutation S sus-mentionnée correspond à l'inversion sur cet ensemble.
La permutation P est spécifiée comme étant une opération très simple, s'implantant
facilement. L'élément ai correspond à l'élévation à la puissance i d'un élément du corps. De telles considérations permettent d'implémenter très efficacement l'AES.
Comme l'AES ne comporte que des opérations très simples sur les
octets, cette propriété lui procure deux énormes avantages :
- l'implantation, même software d'un AES est extrèmement rapide. Par exemple, une implantation en C++ sur un pentium à 200Mhz permet de chiffrer 70Mbits/s ;
- la résistance d'AES à la cryptanalyse différentielle et
linéaire ne dépend pas du choix de S-box comme dans le
DES, qui avaient été suspectées d'avoir été piégées par la
NSA. En effet, toutes les opérations effectuées sont des
opérations simples.
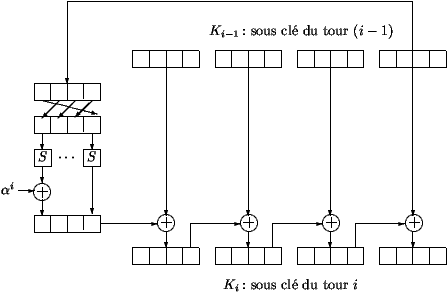
Table 3: algorithme de cadencement de clés
Cryptographie à clé publique
En 1976, Diffie et Hellman publièrent un article ``New Directions in
Cryptography'' qui fit l'effet d'une
bombe dans la communauté des cryptographes, en introduisant le concept de cryptographie à clé publique.
Les algorithmes de chiffrement à clé secrète, les seuls connus
jusqu'alors ne satisfaisaient plus les les besoins nouveaux qui
apparurent parallèlement à l'explosion des moyens de communication
très impersonnels -- le développement des réseaux par exemple.
La solution tout à fait novatrice qu'ils proposèrent fut d'introduire la notion de fonction à sens unique avec trappe ou trapdoor one-way function. C'est une fonction qui se calcule facilement dans un sens, mais qui est calculatoirement impossible à inverser si l'on ne connaît pas un secret appelé trappe,
bien que cette fonction soit connue de tous.
La clé publique est alors la fonction, tandis que la trappe, connue d'un nombre restreint d'utilisateurs
s'appelle clé privée. Ainsi naquit le monde d'Alice, Bob et compagnie. Alice et Bob sont deux personnes
qui cherchent à communiquer de maniere intègre tandis que des personnes peuvent s'interposer, écouter ou
même brouille le canal de communication.
Pour déchiffrer le message le destinataire inverse la fonction en utilisant la trappe.
Le plus bel exemple de cryptosystème à clé publique et sans conteste le plus simple apparut juste deux ans plus tard en 1978. Il est dû à Rivest, Shamir et Adleman d'où le nom RSA. Il s'appuie sur la difficulté de factoriser deux entiers. La clé privée est constitué du triplet (p,q,d) où p et q sont deux nombres premiers de même taille, et ou d est un nombre entier premier avec p-1 et avec q-1. La clé publique se compose de la paire (n, e ).
où n=pq et où e est l'inverse de d modulo (p-1)(q-1), i.e.
ed = 1 mod(p-1)(q-1).
Supposons qu'Alice souhaite envoyer un message chiffré avec la clé publique de Bob (n,e). D'abord, elle
transforme le message en un nombre m inférieur au modulo n. Ensuite elle calcule
c = me modn,
et envoie c à Bob. Celui-ci dont la clé publique est (p,q,d) calcule
cd modn = med modn = m.
Dans le cas de RSA, la fonction à sens unique avec trappe que l'on
considère est la fonction qui affecte à un nombre x <n
la valeur xe modn.
Depuis le système de chiffrement RSA, bien d'autres systèmes de
chiffrement à clé
publique furent développés. Un des plus en vogue
actuellement, et un concurrent sérieux de RSA est un système de chiffrement
fondé sur des problèmes de calcul de logarithmes discrets.
De l'utilisation moderne de la cryptographie
En réalite, l'intérêt de la cryptographie à clé publique est de pourvoir à tout un nombre de problèmes
de sécurité, et d'offrir une très grande souplesse. Celle-ci permis
notamment de trouver des solutions
aux problèmes d'authentification :
- L'identification de personnes :
avec l'apparition des moyens de communication impersonnels,
Alice veut être sûre que la personne avec laquelle elle
communique ne triche pas sur son identité, c'est-à-dire que quelqu'un
prétendant être «Bob» est bien Bob en réalité. Pour ce faire, elle
utilise ce qu'on appelle un protocole d'identification. Il en existe une
multitude reposant sur les mêmes principes qui régissent RSA ou les systèmes utilisant des
propriétés de logarithme discret.
- L'authentification de documents : une autorité peut
authentifier des documents par l'intermédiaire d'une signature
numérique. La signature consiste à
adjoindre au document un certain nombre de bits qui sont calculés en
fonction du document et de l'autorité, et en général sont hachés par une fonction de hachage de type
MD5 ou SHA. De plus, toute personne ayant
accès au document, doit pouvoir vérifier que la signature est bien
celle de l'autorité. Pour ce faire on utilise ce que l'on appelle des schémas de signature.
Un des plus célèbre, le schéma de signature ElGamal repose encore sur des problèmes de recherche de
logarithme discret.
En outre, comme la cryptographie à clé secrète, la cryptographie à clé publique permet d'élaborer des
systèmes de chiffrement, d'assurer la confidentialité des
communications.
Supposons qu'Alice souhaite communiquer avec Bob de manière
privée. Alice trouve dans l'annuaire la clé publique de
Bob, puis chiffre le message avec cette clé. Quand Bob reçoit le
message chiffré, il utilise sa clé privée afin de
déchiffrer le message et de retrouver le texte
clair. Les deux clés ont des rôles fondamentalement
différents, et c'est la raison pour laquelle on parle encore pour
de tels systèmes de cryptosystèmes asymétriques, par
opposition aux cryptosystèmes à clé secrète utilisant la même clé
en chiffrement et en déchiffrement et qui sont également appelés
cryptosystèmes symétriques.
La cryptographie à clé publique possède ici aussi un avantage
majeur sur la cryptographie à clé secrète.
En effet, si n utilisateurs souhaitent
communiquer par le biais d'un cryptosystème à clé secrète, chacun
d'eux doit disposer d'une clé différente par personne du
groupe. Il faut donc pouvoir gérer en tout n(n-1) clés.
Sachant que n peut être de l'ordre de plusieurs milliers, il
faut gérer des fichiers de plusieurs millions de clés. De plus, ajouter un utilisateur au
groupe n'est pas une mince affaire, puisqu'il faut alors engendrer
n clés pour que le nouvel utilisateur puisse communiquer avec
les autres membres du groupe, puis distribuer les nouvelles clés à
tout le groupe. En revanche, dans le cas d'un
cryptosystème asymétrique, on stocke
les n clés publiques des utilisateurs dans un annuaire. Pour rajouter un
utilisateur, il suffit qu'il mette sa clé publique dans l'annuaire.
Clé publique ou clé secrète, un compromis
Dans le paragraphe précédent, on a vu que la cryptographie à clé
publique apportait une solution à bien plus de problèmes que la
cryptographie à clé secrète. Alors on peut se demander quelle est
l'utilité de l'AES dans ce cas. Il existe deux raisons fondamentales à
ce choix.
- D'une part une raison pratique. En effet, la plupart des
systèmes de chiffrement à clé publique sont très lents. Le RSA est
par exemple plusieurs centaines de fois plus lent que l'AES en
programmation logicielle et est complètement hors du coup en
implantation matérielle. A notre époque où la vitesse de
transmission de l'information constitue un enjeu crucial,
l'algorithme de chiffrement ne doit pas être le facteur limitant.
- D'autre part du point de vue de la sécurité se posent des
problèmes relatifs à la structure même des systèmes de chiffrement
à clé publique.
Il est frappant de constater que la taille des clés nécessaire en
cryptographie à clé publique pour assurer une sécurité satisfaisante
est plus grande que la taille des clés en cryptographie à clé
secrète. En fait la notion et l'importance de la taille de clé pour
assurer la sécurité n'est légitime que dans le cas de la clé
secrète. En effet ces systèmes reposent sur l'hypothèse que les
seules attaques possible sont ce que l'on nomme les attaques
exhaustives qui consitent à énumérer toutes les clés possibles.
Par exemple dans le cas d'une clé de 128bits, la
taille de l'espace à énumérer est 2128.
En revanche dans le cas de la clé publique, la taille de clé n'a de
légitimité que lorsqu'on considère le même système. En effet, par
exemple le système RSA de 512 bits est bien moins sûr qu'un AES de 128
bits. La seule mesure légitime pour évaluer un cryptosystème à clé
publique est la complexité de la meilleure attaque connue. Ce qui fait
toute la différence on n'est jamais à l'abri de percées théoriques.
Très récemment un groupe de chercheurs est parvenu à
factoriser un nombre de 512 bits. En conséquence, pour avoir une
sécurité suffisante pour les années à venir, on conseille généralement
d'utiliser des nombres n de 1024 bits.
En chiffrement, il vaut donc mieux utiliser des algorithmes de
chiffrement à clé secrète quand c'est possible. Une solution tout à
fait intéressante et acceptable est le compromis élaboré par
Zimmermann pour concevoir PGP. Le principe du chiffrement est le
suivant : supposons qu'Alice et Bob souhaitent communiquer de manière
intègre, en utilisant un algorithme à clé secrète - en l'occurence,
pour PGP, c'est l'algorithme IDEA.
- Alice et Bob se mettent d'accord sur la clé secrète par un
protocole d'échange de clés. Ce genre de protocole utilise des
propriétés de cryptographie à clé publique. Un des plus célèbres
en la matière est le protocole de Diffie-Hellman.
- Ensuite ils communiquent en utilisant l'algorithme IDEA qui
est publique.
Une fois que leur conversation est terminée, ils jettent la clé de
session. Un tel système combine les avantages des deux types de
crytographie. En général, on considère que le maillon faible est le
protocole d'échange de clés.
Bibliographie
Histoire de la cryptographie :
- S. Singh : Histoire des codes secrets. Jean-Claude
Lattès, 1999.
- D. Kahn : The Codebreakers: the story of secret
writing. MacMillan publishing, 1996.
Pour l'AES :
Cryptographie en général :




